Saltburn感想
最近この人のお勧めする映画を時々観ていて外れがない。その中で観た『saltburn』という映画がなかなか心臓を抉る内容だった。忘れないうちに雑多な感想を残しておこうという目的で書いているので、ネタバレ前提の投稿になるし、見て貰うための推薦コメントというよりも個人的メモ書きのような投稿だ。
#未体験ゾーンの映画たち
— ゆいちむと映画 (@yui_mov) 2023年12月24日
『暗い欲望によって陰キャが“肉食動物”として覚醒してゆく生態系の確率変動』
オックスフォード大学に通う学生オリバーは学内で自分の居場所を見つられずに苦労していた。
そんな彼の前に、貴族のような暮らしを送る裕福な学生フェリックスが現れる。… pic.twitter.com/wQ0t0ssvv8
どんでん返し痛快コメディではない
確かにこの作品は最後にちょっとしたどんでん返しがあり、人によっては「庶民が貴族階級に一矢報いる痛快コメディだ」と解釈する人もいるだろう。しかし自分には、”痛快”というよりも「最後までオリバーが孤独に見えるように描写されていた」という印象の方が強い。人が死んだ後のオリバーは本当に哀しそうにしているし、最後の裸踊りのシーンも画面は暗いからだ。勿論、本当に「友達になりたかっただけ」を描くつもりであれば、一つめの事件で話を終えていただろうから、アンビバレントな主人公を描きたかったと解釈するべきだろう。映画レビューサイトでは”どっちつかずでモヤモヤした”というコメントもあったが、まさにそれが正しい受け止め方だと思うし、そのモヤモヤが持続することで記憶に残る映画だと思う。
とにかく気持ち悪いから平静で観ていられる
オリバーは挙動不審で仲間外れの陰キャで、最初にできた友達が病的で、、という最悪の境遇からスタートする。”既存の仲良しコミュニティの仲間に入れてもらえない”という描写はコミュニケーション能力が低い人にとっては(いや普通の人はみんなそうだと思うが)心をえぐってくる描写だ。自転車を貸してあげる過剰な優しさだとか、自暴自棄になっている友達の異性友達とワンチャン狙おうとする卑怯さだとか、オリバーの人との距離感の異常性から始まるオリバーの気持ち悪い描写は、徐々に気持ち悪さが逸脱し始め、友達の姉とできちゃう・友達のお母さんをたしこむ・バスタブを舐める・実は噓ついてた等々にエスカレートしていく。これは「何か普通じゃねーなこの主人公」という伏線にもなっているが、「こいつは自分とは違う、異常な奴だ、自分はこうじゃない」と”もしかすると自分だったかもしれないオリバー”から”自分とは違う異常なオリバー”へと変わることで、心が抉られていた視聴者からすると、感情移入せずに客観的に受け止めることのできる主人公へと描写が変わっていく。最後までオリバーがただのコミュニケーション能力が変な人のレベルだったら、もっと重たい作品になっていただろう。おかげで安心して見ることができる。
いとこの役割も大きい
ファーリーという”いとこ”が出てくる。オリバーのことが最初から嫌いだしフェリックスを取られるのもムカついているし仕方なくオリバーとも適度に会話するという屈折した心理状態におかれるオリバーもまた、仲の良い友達に別の仲の良い友達ができてしまうことへの嫉妬というよくあるケースの描写になっていて、コミュニケーション能力が低い人の典型のようで重たいのだが、オリバーとファーリーの対立軸があることで、この先どうなるのだろうか?というわかりやすい描写になっている。
変人家族が後半のクッションになっている
何もかも完璧なフェリックスと違って実家の家族は全員異常だ。使用人もロボット過ぎるし、母親は距離が近すぎるし、父親もズレすぎているし、姉もスキモノ過ぎる。毎日ダラダラと誰も仕事をしない(貴族だって仕事はするだろ)様子や派手すぎるパーティーなど、非現実感の高いシーンが現実と非現実の境を曖昧にしていくことで、後半の狂気にスムースにつながっているのだが、急に変にならないよう家族も変人にしておくことで、効果的なクッションになっている。 あと、社会人生活が長くなると、ちょっと距離が変な危ない人、というのもときどき会うので、これはこれで共感ポイントでもある。
映像も音も選曲もいい
脚本の流ればかりの感想になってしまったが、映像も音もいい。異様な作品なのに奇をてらったカットはなく全体的に落ち着いている。冒頭の入学シーンで必要以上に周囲の賑やかな様子が描かれている対比構造もエキストラの費用を考えるとなかなかのコストをかけて作っているし、気がつきにくいがどても凝ったシーンばかりで、とてもバランスがいい。 大学シーンやサマーバケーションで流れる明るい選曲や重いシーンのBGMの組合せもよくできていると思う。
2周するには精神的な負担が多いのだが、なかなか印象深い作品だった。
Pythonで救急車のサイレンの音を作り、Blenderでドップラー効果をかける
救急車のサイレンを作ってドップラー効果をかける必要があったので備忘録。Pythonでモノラルのサイン派を作り、Blenderでドップラー効果をかけるのが最も楽だろうと判断した
Pythonで救急車のサイレンを作る
救急車のサイレン
救急車のサイレンの音は960 Hz と 770 Hzが0.6秒毎に切り替わっているらしい(実を言うと他では1.3秒という記載もあり、ちゃんと元の法令を調べていないので、正確なところは保証しない)。
救急車の位置情報をサイレン音に載せて周囲のカーナビに表示 | NICT-情報通信研究機構
音楽ソフトではこのような周波数を決め打ちで音を作るのは難しいので、Pythonで元の音を作るのが手軽である。
ライブラリのインポート
numpyとwaveだけでよい。
import numpy as np import matplotlib.pyplot as plt #グラフ表示用 import wave
数値の指定
再生する時間、サンプリングレート、作りたいサイン派の周波数、切り替わり秒数、などを変数に入れておく
Amp = 1 #振幅。-1~1で正規化したデータを作るので1にしておく。 fs = 44100 #サンプリングレート(Sampling Frequency) f1 = 960 #サイレンの周波数1(単位:Hz) f2 = 770 #サイレンの周波数2(単位:Hz) sec = 1*60 #再生させる時間(単位:秒) nframe = np.arange(0,fs*sec) #フレーム数=サンプリングレート*秒数 nframe_1term = np.arange(0,int(fs*0.6)) #サイレンの周波数は0.6秒毎に周波数が切り替わる。その1回分
それぞれの周波数1回分のサイン波を作る
python上での時刻というかx軸にあたるものは秒単位ではなくサンプリングレートの1フレームが単位になる。すっかり学生時代の記憶が薄いのでこちらのサイトを見て思い出した。
sin(「角速度(2pi*周波数Hz)×秒数(=フレーム数/サンプリングレート)」)ということになるので、それぞれの周波数のサイン派は以下のようになる。
sin_wave_1_1term = Amp*np.sin((2*np.pi*f1)*(nframe_1term/fs)) sin_wave_2_1term = Amp*np.sin((2*np.pi*f2)*(nframe_1term/fs))
冒頭をグラフにすると以下のようにサイン派になっていることがわかる。(0.6秒だと0で終わらなくない?というのが気になるが、目をつむる。)
fig,ax = plt.subplots(2,1,figsize=(16,9),dpi=500)
ax[0].plot(sin_wave_1_1term[0:120],label="960Hz")
ax[0].plot(np.zeros(120))
ax[1].plot(sin_wave_2_1term[0:120],label="770Hz")
ax[1].plot(np.zeros(120))
ax[0].legend(loc="upper left")
ax[1].legend(loc="upper left")
plt.savefig("sin_wave_1term.svg")
plt.savefig("sin_wave_1term.pdf")
plt.close()

2つのサイン派を連続させて1セット分を作る
sin_wave_1term = np.concatenate([sin_wave_1_1term,sin_wave_2_1term],axis=0)
再生させたい秒数分このセットを繰り返す
ここでもフレーム数があくまで時間の単位になる
sin_wave = np.tile(sin_wave_1term,int(fs*sec/len(sin_wave_1term)))
Waveファイルにするにあたって整数にする。(int16を採用)
WAVEファイルはバイナリーなデータが書き込まれるのでsin派の小数点以下の数値は全て整数にしなければならない。pythonの整数型には精度が異なるものがあるのでどれを採用するかで何桁まで再現できるかが変わる。
sin_wave_frames = np.array(sin_wave*(2**15-1)).astype(np.int16)
Waveファイルに書き出す
どのライブラリを使うかは好みがわかれる。今回はこの時点ではモノラル音源で問題ないので標準ライブラリで完結してしまうのは面倒ではない。
wavの仕組みと読み込み・書き出し方法【pythonで音響信号処理】 | もろみ先輩の日常
量子化ビット数はだいたい16bitなので16bitにしておく
output_file = "original_siren.wav" file = wave.open(output_file,"wb") file.setnchannels(1) # モノラルで良い file.setsampwidth(2) # 量子化ビット数 16bit/8=2 file.setframerate(fs) file.writeframes(sin_wave_frames) file.close()
Blenderでドップラー効果をかける
Blenderにはスピーカーを配置することができる。更にそのスピーカーに音源データを配置できるので、スピーカーを時刻ごとに異なる位置に存在するようにキーフレームを打っておけば、自動的にドップラー効果が反映されたステレオ音源にすることができる。
スピーカーに配置する音源データは後で長さを変えることができないので、元の音源の長さは余裕をもった長さにしておく方が賢明。
スピーカーの配置
カメラなどと同様のところからスピーカーが設置できる
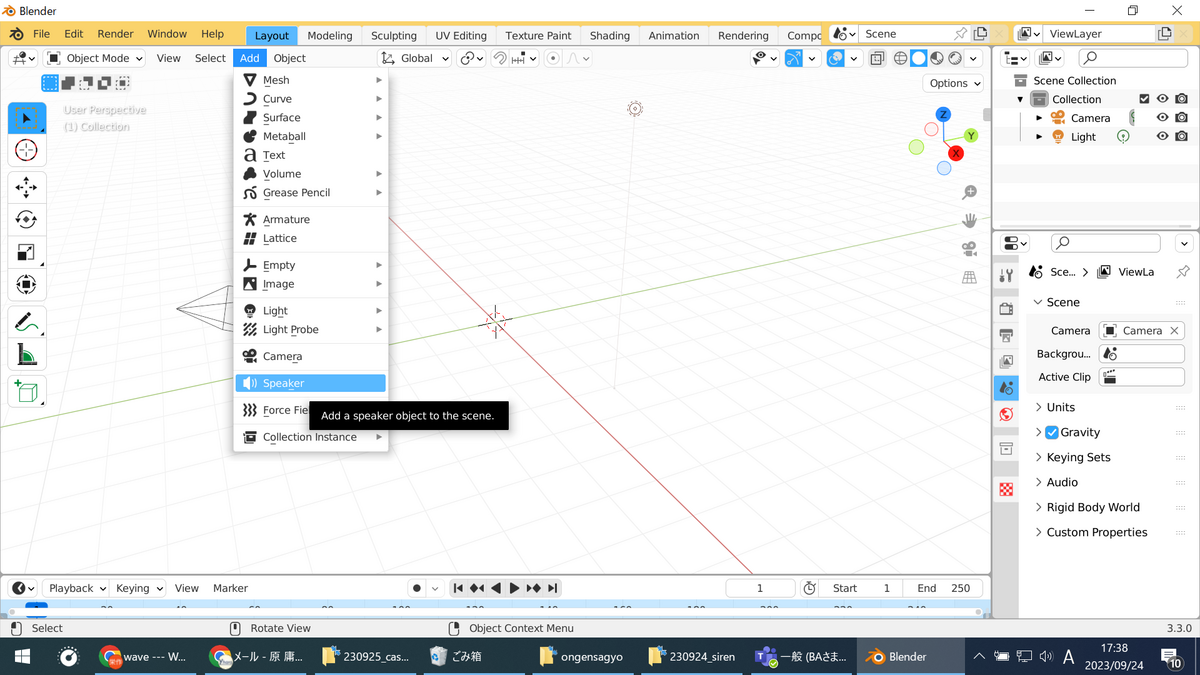
音符マークのプロパティからファイルを挿入できる

スピーカーを何軸上を動かすのか?自分(=カメラ)との距離は?などを考えてカメラの位置や向きを変える。なおスピーカーと近すぎるとちゃんとノイズが入るので、ちょっと遠くしておくのが良さげ。

スピーカーの移動
1フレーム時点で、x軸上で「-15m」の位置とした。どれくらいの時速にするかは決めの問題。

動画のフレームレートを30fpsにしたので、3秒=91フレ時点でx軸上「0m」の位置にあるようにした。自分がわかりすいようにここにキーフレームを打っているが、実際には動画の頭と最後に打っておけば良い。

動画の最後1801フレで135mとした。

音の書き出し
レンダリング設定でステレオにできる。音だけで良いのでno videoにしておく。

音だけをレンダリングできる
参考動画
以上の工程で作った「ドップラー効果なし」「ドップラー効果あり」の音を並べた動画。
Blenderでドップラー効果をかけた時点で一度カメラを通した音の記録になっているので、音量バランスが元の素材より概ね小さくなっているので、2つ並べるときは音量の調整が必要。
Pythonコード全体
# -*- coding:utf-8 -*- import numpy as np import matplotlib.pyplot as plt import wave # 数値の指定 Amp = 1 #振幅。-1~1で正規化したデータを作るので1にしておく。 fs = 44100 #サンプリングレート(Sampling Frequency) f1 = 960 #サイレンの周波数1(単位:Hz) f2 = 770 #サイレンの周波数2(単位:Hz) sec = 1*60 #再生させる時間(単位:秒) nframe = np.arange(0,fs*sec) #フレーム数=サンプリングレート*秒数 nframe_1term = np.arange(0,int(fs*0.6)) #サイレンの周波数は0.6秒毎に周波数が切り替わる。その1回分 # それぞれの周波数1回分のサイン波を作る # 角速度(2pi*周波数Hz)×秒数(=フレーム数/サンプリングレート) # http://izumi-math.jp/M_Sanae/Fourier/four_1_2.htm sin_wave_1_1term = Amp*np.sin((2*np.pi*f1)*(nframe_1term/fs)) sin_wave_2_1term = Amp*np.sin((2*np.pi*f2)*(nframe_1term/fs)) # グラフで確認 fig,ax = plt.subplots(2,1,figsize=(16,9),dpi=500) ax[0].plot(sin_wave_1_1term[0:120],label="960Hz") ax[0].plot(np.zeros(120)) ax[1].plot(sin_wave_2_1term[0:120],label="770Hz") ax[1].plot(np.zeros(120)) ax[0].legend(loc="upper left") ax[1].legend(loc="upper left") plt.savefig("sin_wave_1term.svg") plt.savefig("sin_wave_1term.pdf") plt.close() # 2つのサイン派を連続させて1セット分を作る sin_wave_1term = np.concatenate([sin_wave_1_1term,sin_wave_2_1term],axis=0) # 再生させたい秒数分このセットを繰り返す sin_wave = np.tile(sin_wave_1term,int(fs*sec/len(sin_wave_1term))) # Waveファイルにするにあたって整数にする。(int16を採用) # https://qiita.com/Oka_D/items/86db73ab54dd7b4bc72b # https://qiita.com/Oka_D/items/34e9f6c47962f51946c1 sin_wave_frames = np.array(sin_wave*(2**15-1)).astype(np.int16) # Waveファイルに書き出す # https://moromisenpy.com/python_wav/ # https://qiita.com/Dsuke-K/items/2ad4945a81644db1e9ff # https://docs.python.org/ja/3/library/wave.html output_file = "original_siren.wav" file = wave.open(output_file,"wb") file.setnchannels(1) # モノラルで良い file.setsampwidth(2) # 量子化ビット数 16bit/8=2 file.setframerate(fs) file.writeframes(sin_wave_frames) file.close()
フェティシズムを消費する
作家の創作過程が綴られた本を比較的近い期間のうちに2冊読んで、気がついたことがある。
小説家の方では、自分の好きな作風の作家の本を何度も読めというアドバイスや、物語に登場させたい登場人物の顔写真ないしイラストと設定情報を壁に貼り暫く脳内で妄想を続けろというアドバイスなどがあった。
作曲家の方では、好きな曲をひたすら耳コピしてみろというアドバイスや、作業台には自分が好きなものを集めて”どういうときに心を揺さぶられたか?”を思い出して創作のヒントにしろというアドバイスなどがあった。
所謂テクニックや文法を紹介する類の本ではなかなか言及されることのない重要なアドバイスだと思う。
実は最近自分も”何かこの作品よかったな”と思ったアニメを2周して、どこに良さを感じたのか?を味わうということをしている。そんなことをしていると一生の間に観られる作品数に限りが出てしまうのだが、2周すると1周目で無意識に感動してい演出に意識的になれる。自分の性癖を掘り返しているような気持ち悪さもあるのだが、”創作物を消費するというのは自分のフェティシズムを消費すること”なんだなと思うと妙に納得感を覚えてきた。
作家の自己表現を消費しているというよりも、作家のフェティシズムを消費しているという感覚だ。だから同じフェティシズムを再現してさえくれれば、作家が誰であっても構わない。
実はビジネスにおいてもフェティシズムは重要ではないかと思っている。会社組織は生産設備・特許・知見といった蓄積に差はあるものの元はただの人間の集まりでしかない。それがいつの間にか他社に真似のできないサービス提供に行き着くのは、創業者や歴代社長に独自の執念があって何かにフォーカスした結果、差別化できているのだと思う。何かに執拗なまでに拘るということは、生き残っていく上で重要なスキルなのではないだろうか。
D・N・A²(アニメ版)_感想
D・N・A²のアニメ版を初めて観た。
原作も好きなのだがアニメ版も不思議によくできた作品で、今まで観ていなかったのが勿体ない。
まず撮影が美しい。セル画の頃の綺麗な撮影処理は本当に光っているように見える。
次に背景のトンマナが良い。1話の佐伯倫子の部屋の壁が何故かカラーグラデーションになっていたり、夕方であることが必須でもないようなシーンで敢えて夕方感のある空になっていたり、パステルカラーが映えている。
OPが曲も画面もよい。このOPで改めてL'Arc〜en〜Cielの楽曲のクオリティの高さを発見した。OPの画面もよくできていて、空の中に縦に細長い窓枠を置いてそこに葵かりんを座らせるカットなんかよく思いつくものだ。
BGMの選定や強弱もあっている。違和感がないし、盛り上がるところで音が大きくなっていたり、調整に的確さを感じる。(1話のED楽曲の崩しが先に劇中で使われていることにも気がついたが、よくレコード会社がOKしたと思う。何ならEDのシャ乱Qがチンピラ役で出演しているのも、どうやって成立したのか不思議な配役だ)
何よりも、桂正和キャラクターのヒロインの表情に気合が入っていて、アップのシーンの絵面やたそがれているシーンの絵面が良い。
ストーリーだけをピックアップしてしまうと、なぜこの主人公がモテるのかの経緯に強引さがあるし、真面目にやりたいのかギャグに振り切りたいのかどう観ていいのかよくわからないし、妙にことみの回が長すぎるし、子安武人さん演じる変人キャラはもはややり過ぎくらいに浮いているのだが、全体的な印象としては謎に拘りの強いよくできた作品だった。
物語を強制的に終わらせるなら”大ダコ”
この記事はネタバレを含みます
東宝特撮シリーズの名作の一つに『フランケンシュタイン対地底怪獣』という作品がある。エンディングが複数パターン存在することで有名なのだが、何よりそのエンディングが衝撃的なことで有名だ。
「あっ!大ダコだ!」
多分そんな台詞だった。フランケンシュタインと地底怪獣バラゴンが死闘を繰り広げた直後、海から大ダコが登場しフランケンシュタインを海に引きずりこんでエンディングになるという唐突感のある終わり方なのだ。
本作のフランケンシュタインは手首だけからどんどん再生し巨大化し人間の手に負えない怪物になり人々に恐れられながらも、心優しい側面を持ち、共通の敵たる地底怪獣までやっつけてくれる、というキャラクター設定なのだが、”人間の手に負えない存在”という設定である以上、「人間と仲良くなりましたとさ」という結末には持って行けず、消滅して貰うしかない。
しかも、手首だけから再生できるので地底怪獣と相打ちして絶命させるというのも難しい。ゆえに、大ダコが海に引きずり込んで人間の世界からフェードアウトさせる、という強制的な手段は理にかなっている。
唐突に新しい課題をクライマックスに持ってくるのはレアではない
最近になって『オーバーマン キングゲイナー』という作品を見た。とても面白い作品だ。
キャラクターはそれぞれの事情や正義を抱えて登場し、主人公も主人公の周りに居る人も、襲撃してくる敵対勢力も、それぞれに共感できるところがある。途中で死んでしまうキャラクターも居るが、敵対してきたキャラクターたちの殆どが死ぬこともなければ主人公側と決着をつけることもなく最終話を迎える。
感情移入してしまった敵側のキャラクターを死なせたり主人公側と決着をつけて白黒つけてしまうよりは、全く別の課題を発生させ、それを解決させることで、物語のエンディングを迎えよう、という設計になっている。(主人公たちが乗っていたロボットのようなものオーバーマン/デビルのうちの一つが暴走し心を支配してしまう、という課題が提示される)
この作品を見ていたときに「これは大ダコと同じだ」と感じた。ところどころ伏線がある点では、キングゲイナーの方が優れたプロットだが、得体の知れない謎の敵や、暴走する巨大破壊兵器などを最終話付近に登場させて物語を”終わらせる”というテクニックは、頻繁に見られるパターンの一つである。
そういう意味では、大ダコはそこまで衝撃的なことではないと思えてきたのだ。
Pythonで画像をA4比率のPDFに分割する
Webサイトのキャプチャはchromeのデベロッパーツールから撮ることができるが、PNGなどの画像ファイルになる。しかし、 PC上で部分的に拡大するにはPDF形式の方が扱いやすいし、紙に出力するのであればA4比率のPDFに分割できた方が便利である。
事前準備
img2pdfとPILを使用する必要がある。以下のサイトを参考にした。(主に1つめ)
コード
必要なライブラリのインポート
import img2pdf from PIL import Image
ファイルの読み込み
いくつもの画像ファイルを変換する必要があるのであるならば、ファイル名を自動で取得し、同じファイル名を使って出力するようにするとよい。コードに直接ファイル名を記述するのは面倒である。
import glob
例えば、inputというフォルダに画像ファイルを入れる想定だと以下のようにファイル名を取得すればよい。
files = glob.glob("./input/*") for file in files: print(file)
A4サイズで分ける
各ファイルについて同じ動作を繰り替えすfor文構文にする。
PILのImage関数は画像サイズを取得できる
横の長さを取得し、A4サイズの比率(210mm x 297mm)を掛ければA4サイズ比率の縦の長さを求められる。ここでは、image_heightとした。
複数枚に分割しそれぞれをPDFにするため、その作業を何回繰り返す必要があるのか、画像の縦の長さをimage_heightで割って、商を求めてプラス1しておくことで求めておく。image_numsとした。
また、吐き出すフォルダ名をoutputとしておき、ファイル名も文字列変換でpngをpdfに、inputフォルダをoutputフォルダにしておけば、同じファイル名で吐き出せる。分割回数をファイル名に"_"などで加えておくとよい。
画像をA4比率で切り抜くにはcrop関数を使う。開始する縦の位置をposとして、繰り返しごとにimage_height分の高さを加えていけばよい。また、切り抜きの終了の縦の位置についてはpos+image_heightだけでも良いが、最後の1枚に余白を残したくなければ、下記のコードのように(「pos+image_height <= image_original.size[1]」)元の画像の長さ以下かそうでないかを判定し、最後の1枚の終了位置を元の画像の高さと同じにしておけば余白はでない。
for file in files: image_original = Image.open(file) image_original = image_original.convert("RGB") image_width = image_original.size[0] image_height = round(image_width/210*297,-3) image_nums = int(image_original.size[1] // image_height) + 1 filename = file.replace(".png","") filename = filename.replace("input","output") pos = 0 for i in range(image_nums): if pos+image_height <= image_original.size[1]: image_part = image_original.crop((0,pos,image_width,pos+image_height)) else: image_part = image_original.crop((0,pos,image_width,image_original.size[1])) image_part_filename = filename + "_" + "{0:03d}".format(i) + ".pdf" image_part.save(image_part_filename) pos += image_height
ウィッチハンターロビンが面白い、けどなぜなのかはわからない
最近になって、「ウィッチハンターロビン」を観た。
登場人物はボソボソと喋り、少しサスペンス的な要素はあるものの緊張感の連続というわけでもなく、主人公の精神的成長も緩やかなものだ。
画の構成も特別にトリッキーな演出は少ない。
それでも全く飽きない画が連続する。単調に画が連続することがないが、特異なカットが一つもなくどれも自然に感じるカットばかりだ。
「では、このような画の流れを思いつけるか?」と観察しようという意識で2周(目の途中で配信期限が切れた)すると、ついつい引き込まれて観察しきれなかった。恐らく奇をてらうよりも難しいだろう。
因みに後で知ったことだが、「閃光のハサウェイ」と同じ監督だった。この作品も何故か引き込まれて映画館で2周したのだが、この監督のディレクションが自分の好みだということなのかもしれない。




![D・N・A2 ~何処かで失くしたあいつのアイツ~ Collector's Edition [DVD] D・N・A2 ~何処かで失くしたあいつのアイツ~ Collector's Edition [DVD]](https://m.media-amazon.com/images/I/512SE40KGpL._SL500_.jpg)


![オーバーマン キングゲイナー BDメモリアルBOX [Blu-ray] オーバーマン キングゲイナー BDメモリアルBOX [Blu-ray]](https://m.media-amazon.com/images/I/511BW3Z3AuL._SL500_.jpg)
![Witch Hunter ROBIN コンプリート DVD-BOX (全26話, 720分) ウイッチハンターロビン サンライズ アニメ [DVD] [Import] [PAL, 再生環境をご確認ください] Witch Hunter ROBIN コンプリート DVD-BOX (全26話, 720分) ウイッチハンターロビン サンライズ アニメ [DVD] [Import] [PAL, 再生環境をご確認ください]](https://m.media-amazon.com/images/I/51oBsbtZBOL._SL500_.jpg)
