バナー広告の接触回数分布を関数で回帰してみる
広告業界ではある媒体に出稿した時の接触回数の分布（1回当たった人がn人、2回当たった人がn人）をベータ二項分布などで近似しシミュレーションするのが一般的と言われている
なおこのサイトによるとWeb広告の場合は、負の二項分布がグローバルで標準らしい。*1
ということで、バナー広告の接触回数分布がどんな関数になるのか、入手可能なデータで確かめてみた。
ビデオリサーチ社が2年前に調査したデータを使う
データソースについて
説明はここを参照して欲しい。
リリースの最後の方に、接触回数の分布がある。
オンライン広告の認知効果の基準値整備に関するお知らせ | ニュース || コーポレートサイト
このサンプル数がわからなかったが、計算の簡単のためこのパーセンテージの小数点が消えるように桁を変えて,仮にこの値を回帰できる関数を探してみる。
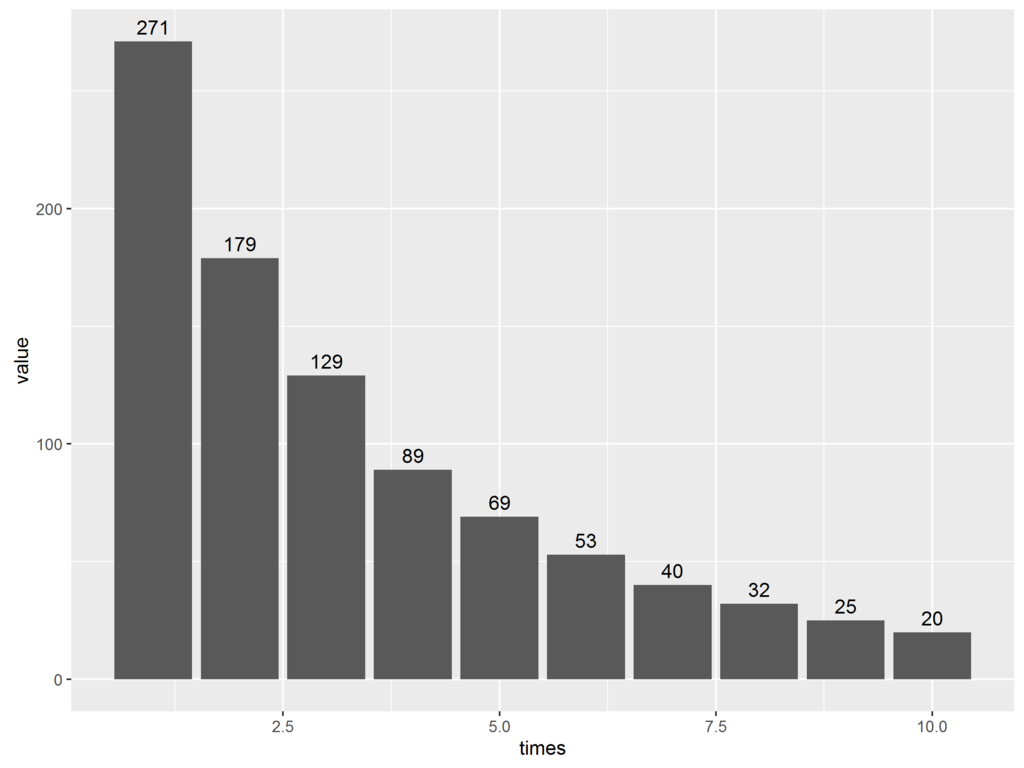
x y 1 271 2 179 3 129 4 89 5 69 6 53 7 40 8 32 9 25 10 20
プロットしてみる
プロットした時の関数は省略する。
一般的に言われている負の二項分布っぽい感じはする。
負の二項分布について
負の二項分布の理解
負の二項分布は、確率pの試行をN回繰り返す時に、r回成功するまでに何回試行を繰り返すか？の分布を知る為に使われるのだが、今回の場合はその理解というよりも、こちらのブログの通り、
http://sugisugirrr.hatenablog.com/entry/2016/01/31/%E7%AC%AC%EF%BC%97%EF%BC%94%E5%9B%9E_%E3%83%9D%E3%82%A2%E3%82%BD%E3%83%B3%E5%88%86%E5%B8%83%E3%81%A8%E3%82%B5%E3%83%83%E3%82%AB%E3%83%BC%E3%81%AE%E3%82%B4%E3%83%BC%E3%83%AB%E6%95%B0sugisugirrr.hatenablog.com
カウントデータの回帰にポワソン分布を使おうとしたら分散がもっと大きい分散なので、ガンマ分布とポアソン分布の階層モデルを作るとき、それが負の二項分布になる、というポアソン分布の過分散時の推定、と言われている方の用途で使う。
このサイトを見ると確かにガンマ分布で何パターンか作ったポアソン分布を合成していくと負の二項分布になっている。。。
http://stat.biopapyrus.net/probability/negative-binomial.html
RStanに負の二項分布のあてはめ
Rのパッケージ、nbGLMでやってもほぼおなじ結果なのだがせっかくなのでRStanでベイズモデリングしてみる。
知識不足のため、収束させる為の条件はわからなかったのでコードはほぼほぼこれらのサイトを見よう見まねで使った。
Simulate and fit negative binomial GLMs in Stan
モデリングのコード
接触回数xを入れたら、接触人数yが予測できるようなモデリングを仮定する。線形回帰と異なってリンク関数なので、y直接ではなく、yの自然対数を回帰する。
log(y) = b0 + b1 * x
モデルのコードは別ファイルにしてもいいが、個人的には同じファイル無いで「""」で挟んで代入する方が見直す時に便利なので好き。
model <- " data { int<lower=0> N; vector[N] x; int<lower=0> y[N]; } parameters { real<lower=0> phi; real b0; real b1; } model { phi ~ cauchy(0,3); b0 ~ normal(0,5); b1 ~ normal(0,100); y ~ neg_binomial_2_log(b0 + b1 * x,phi); } "
データの読み込みとRStan用のリスト化
RStanに受け渡す為にデータをリスト化する
d <- read.csv("banner.csv",header=T) data <- list(N=nrow(d),x=d$x,y=d$y)
実行
実行した後、summary(fit）で先程仮定した「b0」や「b1」の平均値や四分位数が出て来るが、meanを使って値を代入すればよい。
![実践ベイズモデリング 解析技法と認知モデル [ 豊田秀樹 ]](https://thumbnail.image.rakuten.co.jp/@0_mall/book/cabinet/2206/9784254122206.jpg?_ex=128x128 "実践ベイズモデリング 解析技法と認知モデル [ 豊田秀樹 ]")
のコードを見て、”なるほど”と思った。流石です。
fit <- stan(model_code=model,data=data,seed=1234) rs <- rstan::extract(fit) b0 <- mean(rs$b0) b1 <- mean(rs$b1)
暫く待つと以下の値を得た。*2
> (b0) [1] 5.794788 > (b1) [1] -0.2975039
回帰の関数
これで、x（接触回数）からy（接触人数）を予測する関数ができた。log(y)を回帰しているので、ネイピア数に計数を累乗すればいい。
y = exp( 5.794788 + -0.2975039 * x)
元のデータより広い値を入れてみる
恐らくビデオリサーチのデータは、10回よりも多いデータもあった筈だ。（パーセンテージを足すと100%にならない）
そこで、新しく d_predという名前のデータフレームを作り、そこに先程の関数で予測される値を格納し、そのデータと元のデータをdplyrのレフトジョインで一つのデータフレームに入れてみる
x_fit <- seq(1:20) y_fit <- exp(b0 + b1 * x_fit) d_pred <- as.data.frame(NULL) d_pred <- as.data.frame(x_fit) colnames(d_pred) <- c("x") d_pred$y_fit <- y_fit d_pred <- dplyr::left_join(d_pred,d)
> head(d_pred) x y_fit y 1 1 244.02836 271 2 2 181.23247 179 3 3 134.59587 129 4 4 99.96028 89 5 5 74.23747 69 6 6 55.13392 53
余り精度は高くないようだが、これが今の自分の知識の限界なので勘弁して欲しい。
実測値と予測値を並べてグラフにしてみる
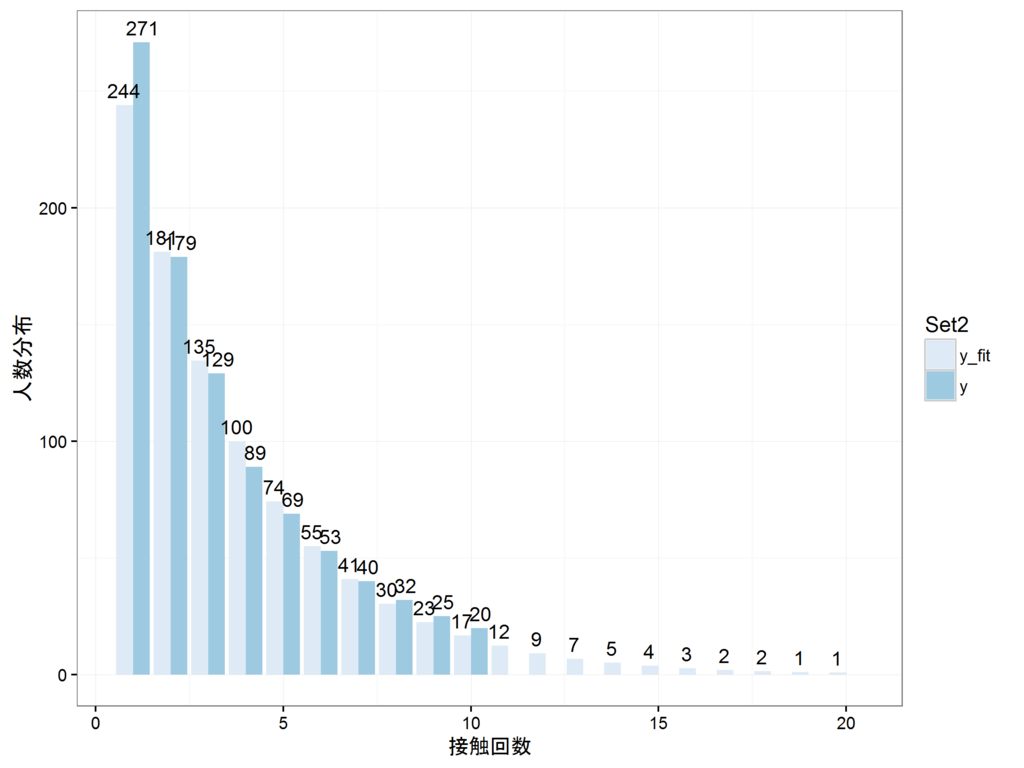
実測値と予測値の棒グラフを並べてみる
p <- ggplot(d_pred_m,aes(x=x,y=value,fill=variable)) p <- p + theme_bw(base_family="Japan1GothicBBB") p <- p + geom_bar(stat="identity",position = "dodge") p <- p + geom_text(aes(x=x,y=value,label=round(value)),vjust=-0.5,position = position_dodge(1)) p <- p + scale_fill_brewer("Set2") p <- p + xlab("接触回数") p <- p + ylab("人数分布") plot(p) ggsave(plot=p,file="20170416-1.png",dpi=300,width=4,height=3,scale=2)
個人的な感覚では、一回しか接触しないバナーが殆どだとは思うけれど、2015年のビデオリサーチの大規模調査を信用するとするとこんな感じである。自分は接触しなくても、ヘビーにWebを使う人ととそうでない人とバラつきがあるということだろう。
媒体数が限られているマス広告と比べて、果してバナー広告の接触回数分布が簡単に回帰できる類いのものなのか？という疑問はあるし、そもそもターゲティングが違えばまた違うだろうし、そもそもリマーケティングを入れたりフリークエンシーキャップをかけたらもっと複雑になるので予測すること自体が難しいのではないか？とは思う。
ただ、「負の二項分布で近似できる」という話については、嘘ではなさそうだ。
